金半接触(对应教材第九章)
-
同质结: 同种半导体材料(如硅-硅)形成的PN结。
-
异质结: 不同半导体材料(如硅-锗,或GaAs-AlGaAs)形成的PN结。
-
金半结: 特指金属与半导体直接接触形成的结构,也被称为肖特基势垒二极管。
-
欧姆接触: 金半接触的特殊情况(或理想情况),指接触界面没有明显的整流效应,电流与电压呈线性关系,在电路中不仅不阻碍电流,反而作为低阻抗的连接通道。
半导体功函数表达式:
eϕs=χ+(EC−EF)s=χ+ϕn
常见材料能量参数表:
| 金属 | **功函数 ϕₘ (eV)** | 半导体 | **电子亲和能 χ (eV)** |
|---|
| Ag, 银 | 4.26 | Ge, 锗 | 4.13 |
| Al, 铝 | 4.28 | Si, 硅 | 4.01 |
| Au, 金 | 5.1 | GaAs, 砷化镓 | 4.07 |
| Cr, 铬 | 4.5 | AlAs, 砷化铝 | 3.5 |
| Mo, 钼 | 4.6 | - | - |
| Ni, 镍 | 5.15 | - | - |
| Pd, 钯 | 5.12 | - | - |
| Pt, 铂 | 5.65 | - | - |
| Ti, 钛 | 4.33 | - | - |
| W, 钨 | 4.55 | - | - |
热力学原理:金属与半导体相接触时,电子将从功函数小的地方跑到功函数大的地方。 系统的热力学平衡要求统一的费米能级。
根据电子流动的方向和半导体表面形成的状态,接触被分为两类:
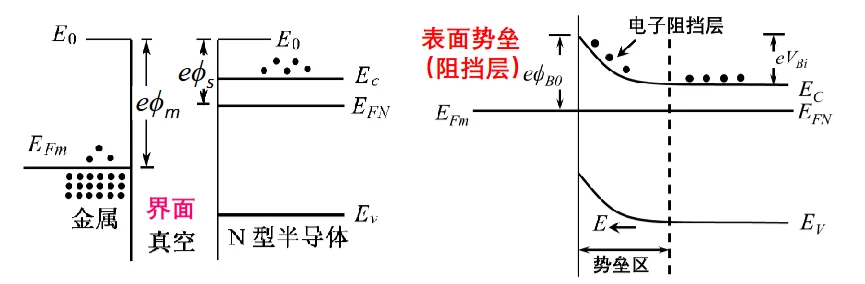
金半接触(和N型半导体)
电荷输运过程:
ϕm>ϕs, 由于 ϕm=E0−EFm 且 ϕs=E0−EFN,不等式 ϕm>ϕs ,可推导出 EFm<EFN。
根据热力学原理,电子从费米能级高的N型半导体流向费米能级低的金属。
空间电荷区的形成:
半导体表面失去电子(多子),留下了带正电的施主离子。这些离子作为晶格的一部分,不可移动。金属表面获得了电子,带负电。
因此,在半导体一侧形成了带正电的空间电荷区(耗尽层)。
能带弯曲与平衡态:
平衡时,整个系统的 EF 必须是一条水平线。对于半导体,电子在表面处的电势能更高。因此,半导体的能带(EC,EV)在表面处向上弯曲。
势垒的形成:
两边的电子进入另外一侧分别需要克服两种势垒:
| 势垒 | 方向 | 表达式 | 补充说明 |
|---|
| 表面势垒eϕB0 | 金属→半导体 | eϕm−χ | 理想情况下,不随外加电压变化 |
| 内建电势差eVBi | 半导体→金属 | eVBi=ϕm−ϕs | 接触前金属与半导体的费米能级之差 |
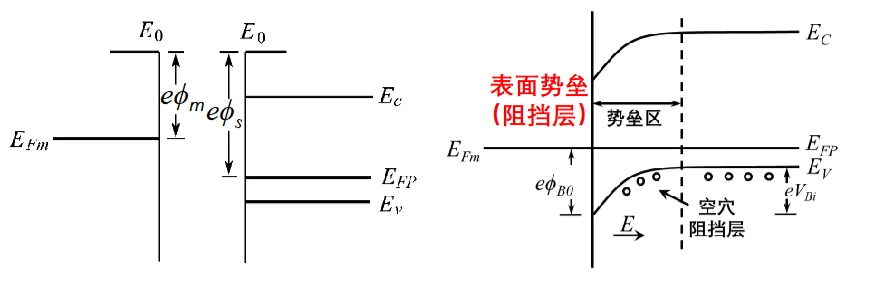
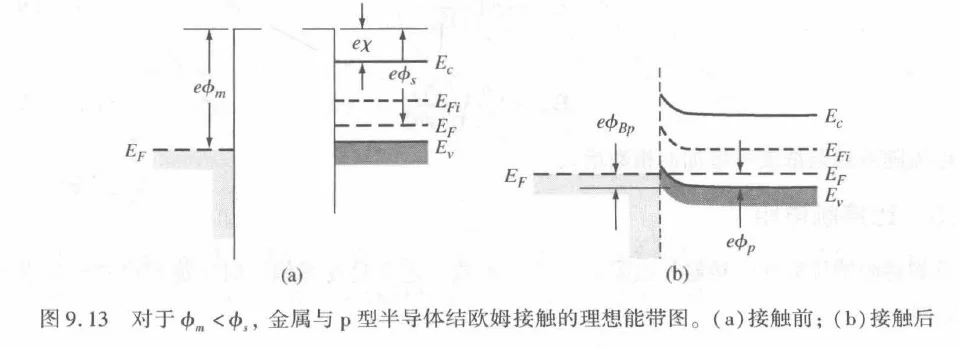
金半接触(和P型半导体)
电荷输运过程:
ϕs>ϕm,意味着 E0−EFP>E0−EFm,即 EFm>EFP
半导体的费米能级低,意味着空穴能量高。电子从金属流向半导体,即空穴从半导体流向金属。这导致半导体表面空穴浓度降低(耗尽)。
空间电荷区与能带弯曲:
半导体表面空穴被耗尽,留下了带负电的受主离子。金属表面带正电。由于半导体表面带负电,这里的电子电势能升高,能带(EC,EV)相对于内部向下弯曲(也就形成了空穴的势垒)。
| 特性 | 金属 - N型半导体接触 | 金属 - P型半导体接触 |
|---|
| 接触前提 | ϕm>ϕs | ϕs>ϕm |
| 费米能级关系 | EFm<EFN | EFP<EFm |
| 载流子输运方向 | 电子从半导体流向金属 | 空穴从半导体流向金属 |
| 空间电荷区 | 半导体一侧形成由带正电的施主离子组成的耗尽层 | 半导体一侧形成由带负电的受主离子组成的耗尽层 |
| 金属侧电荷 | 积累电子,带负电 | 失去电子,带正电 |
| 能带弯曲方向 | 半导体表面能带向上弯曲 | 半导体表面能带向下弯曲 |
| 表面势垒 | eϕm−eχ | Eg+eχ−eϕm |
| 内建电势差 | eϕm−eϕs | eϕs−eϕm |
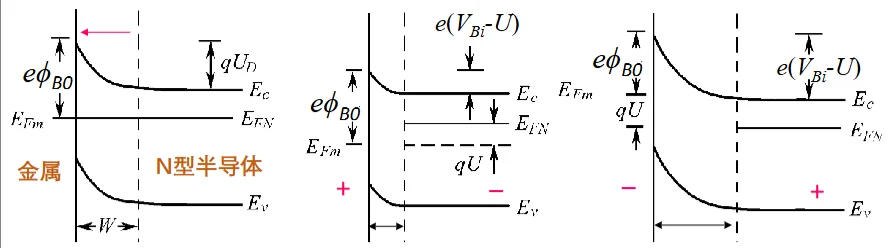
整流效应图解
平衡状态(左图): 电子的双向流动达到动态平衡,净电流为零
系统具有统一的费米能级(EFm 与 EFN 对齐)
正向偏置(中图): 半导体的费米能级 EFN 相对上移,金属费米能级 EFm 相对下移,两者能量差为 qU
半导体侧的能带弯曲量减小。电子从半导体进入金属所需克服的势垒降低为 e(VBi−U), 由于势垒降低,N型半导体中的多子(电子)极易越过势垒扩散到金属中。电子流呈指数级增加,形成很大的正向电流。
反向偏置(右图): EFm 上移,EFN 下移
半导体侧的能带弯曲增强。电子从半导体进入金属所需克服的势垒升高为 e(VBi+U)。半导体中的电子很难越过这个增高的势垒。电流主要由金属流向半导体的电子构成,但金属电子面临的势垒 eϕB0 几乎不变且很高,因此只有极少的电子能跃过,形成微小的反向饱和电流(漏电流)。
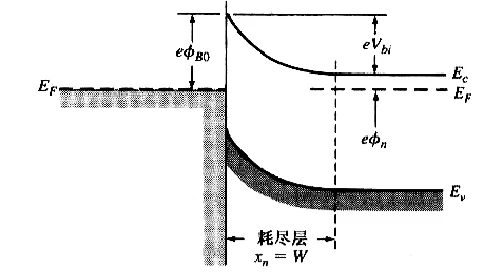
肖特基势垒二极管
肖特基势垒高度 (ϕB0): 也就是金 - N接触的表面势垒
ϕB0=ϕm−χ
理想的肖特基模型下,这个势垒只和材料本身相关。
由泊松方程:
dxdE=ϵsρ(x)
边界条件: 在耗尽层边缘 x=xn 处,电场强度必须连续且归零(中性区无电场),即 E(xn)=0。
电场分布公式:
E=−ϵseND(xn−x)
即耗尽区内的电场呈线性分布,当 x=0(金半界面)时,电场强度绝对值 ∣E∣ 达到最大值。根据电场边界条件,半导体侧存在正电荷区,为了保持电场终止,金属表面必然存在等量的负电荷。
再次对电场 E(x) 积分(或利用泊松方程 dx2d2ϕ),得到内建电势差 Vbi 与耗尽层宽度 xn 的平方成正比(表明电压主要降落在耗尽区,近似单边突变结):
Vbi=2ϵseNDxn2
W=xn=[eND2ϵs(Vbi+Va)]1/2
CT=[2(Vbi+Va)eϵsND]1/2
CT21=eϵsND2(Vbi+Va)
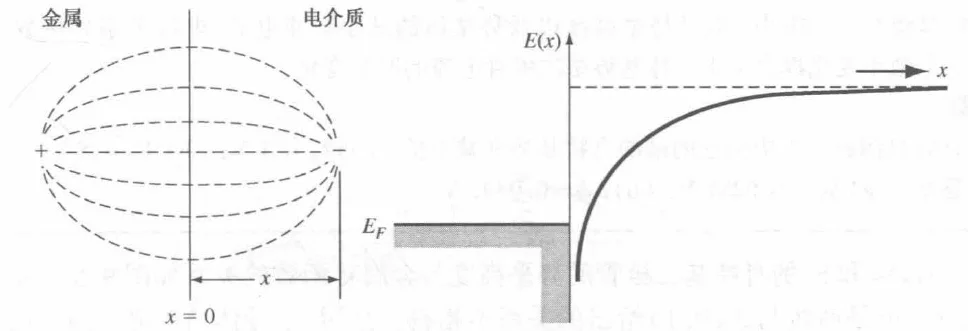
镜像效应
当一个电子(电荷量 −e)处于金属表面外的半导体中,距离界面为 x 时,金属表面会感应出正电荷。等效于在金属内部距离界面 −x 处存在一个电荷量为 +e 的“镜像电荷”。
镜像力引起的电势能 −ϕ(x) :
−ϕ(x)=16πϵsx−e
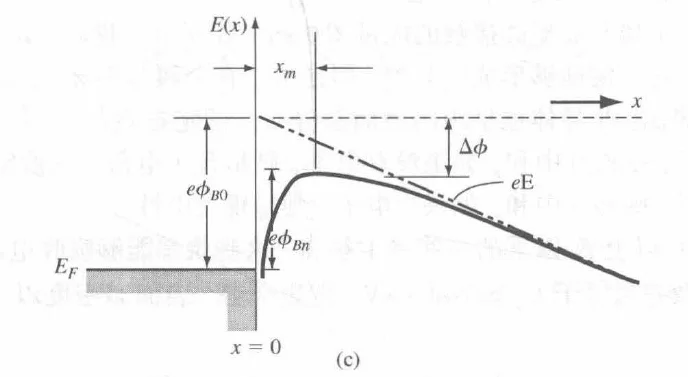
总势能:
−ϕ(x)total=16πϵsx−e−Ex
势垒最高点距离界面的位置 xm(不再位于界面处 (x=0)):
xm=16πϵsEe
肖特基势垒降低量 (Δϕ):
Δϕ=4πϵseE
实际的肖特基势垒高度 ϕBn 将小于理想值 ϕB0,即 ϕBn=ϕB0−Δϕ。且反向偏压越大(电场 E 越大),势垒降低效应越明显,这是导致反向电流随电压轻微增加的主要原因。
半导体表面晶格的中断导致在禁带中引入了连续的能级,称为界面态。界面态的存在使得半导体表面能够通过填充或排空这些能级来调节表面电荷 Qss。为了维持界面整体的电中性,半导体能带的弯曲程度和势垒高度必须自我调整。
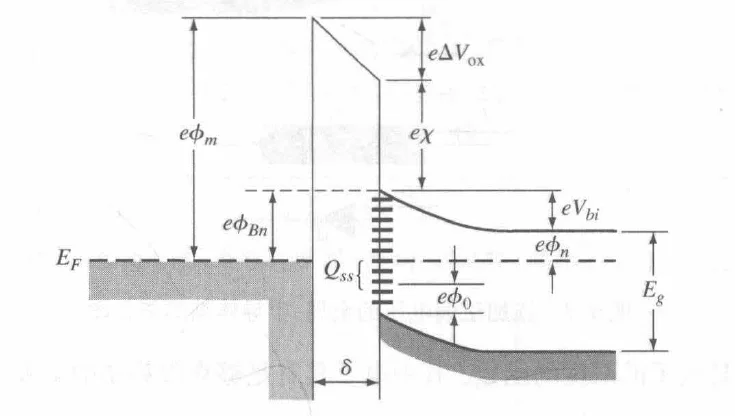
金半结能带图&表面态
| 特性 | 施主型表面态 | 受主型表面态 |
|---|
| 占据/空置时的电性 | 能级被电子占据时呈中性 | 能级空置时呈中性 |
| 电子转移后的电性 | 释放电子后呈正电性 | 接受电子后呈负电性 |
| 中性能级φ₀的界定 | φ₀以下能级为施主态(易释放电子) | φ₀以上能级为受主态(易接受电子) |
| 关键项 Dit(界面态密度),若 Dit→∞(界面态密度极高), ϕBn 将主要由 ϕ0 决定,而与金属功函数 ϕm 几乎无关。 | | |
当界面态密度很高时,费米能级被“钉扎”在 ϕ0(中性能级) 附近,这种现象称为费米能级钉扎。此时势垒高度主要由半导体表面性质决定,而非金属材料。
实验验证:
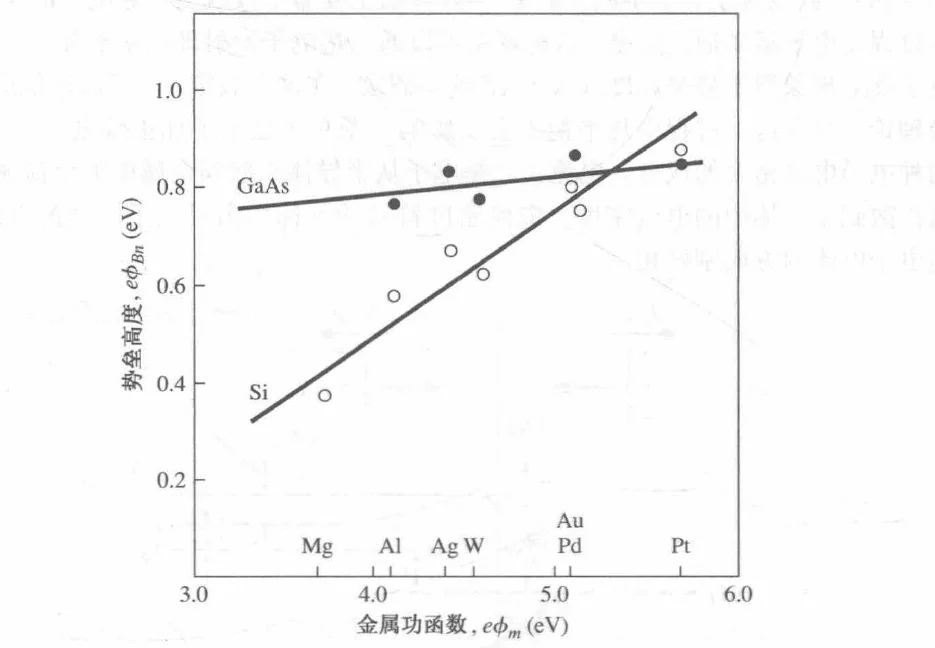
肖特基结主要依靠多子的运动来决定电流。
只有能量高于势垒顶端的那些“热电子”才能越过势垒。电流的大小取决于越过势垒的载流子数目。
电流构成:
- Js→m(半导体到金属): 电子需克服的势垒随外加电压 Va 变化,势垒高度为 e(Vbi−Va)。该电流分量随电压指数变化。
Js→m=A∗T2exp(kT−eϕBn)exp(kTeVa)
- **$A^*$ (有效理查德森常数):** $A^* \equiv \frac{4\pi e m_n^* k^2}{h^3}$,是一个与材料有效质量相关的物理常数。
- Jm→s(金属到半导体): 电子需克服的势垒是 ϕBn(相对固定)。因此,反向饱和电流主要由这一项决定,且在理想情况下与电压无关。
Jm→s=−A∗T2exp(kT−eϕBn)
- 净电流: 外部观测到的电流 J 是上述两股电流的代数和。正偏时 Js→m 占主导,反偏时仅剩微弱的 Jm→s(类似PN结的正向电流和反向饱和电流)。
J=A∗T2exp(kT−eϕBn)[exp(kTeVa)−1]
写成类似PN结饱和电流的形式:
JST=A∗T2exp(kT−eϕBn)
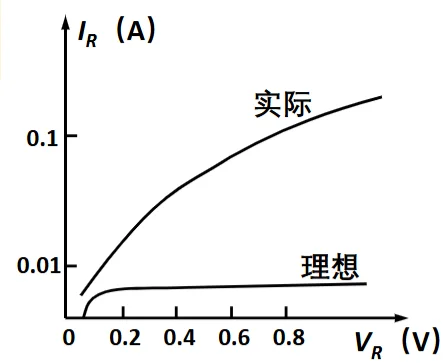
理想-实际电流电压关系图
造成这种非理想特性的原因是肖特基效应。实际势垒高度 ϕBn 并非由 ϕB0 恒定决定,而是受到镜像力降低量的修正,修正后的表达式:
JST∝exp(kTeΔϕ)
| 特性类别 | 肖特基二极管 | PN结二极管 |
|---|
| 反向电流 | | |
| 物理机制 | 热电子发射理论 | 少子扩散理论 |
| 数量级 | 反偏电流比PN结大2~3个数量级,受势垒降低主导。 | 反偏电流密度约10e−7A/cm2(小,受空间电荷区产生电流支配)。 |
| 正向导通特性 | | |
| 导通电压 | ~0.3V | ~0.7V |
| 物理原因 | 反向饱和电流JST远大于PN结JS,由二极管方程,同电流下V更小。 | 反向饱和电流JS小,同电流下需更高V。 |
| 性能总结 | 低压降(低功耗),高漏电(反向电流大)。 | 高压降(较高功耗),低漏电(反向电流小)。 |
| **开关特性(高频)** | | |
| 输运机制 | 多子器件:多子热发射+漂移(无少子参与)。 | 少子器件:少子扩散运动为主。 |
| 电荷存储效应 | 无(无少子注入与积累,几乎无扩散电容)。 | 有(正向导通时少子积累,需时间复合/扩散返回)。 |
| 反向恢复时间 | 极短(纳秒级或更低)。 | 较长(存在反向恢复时间trr)。 |
| 高频特性 | 优异(开关速度快,适合高频)。 | 受限(存储效应限制高频能力)。 |
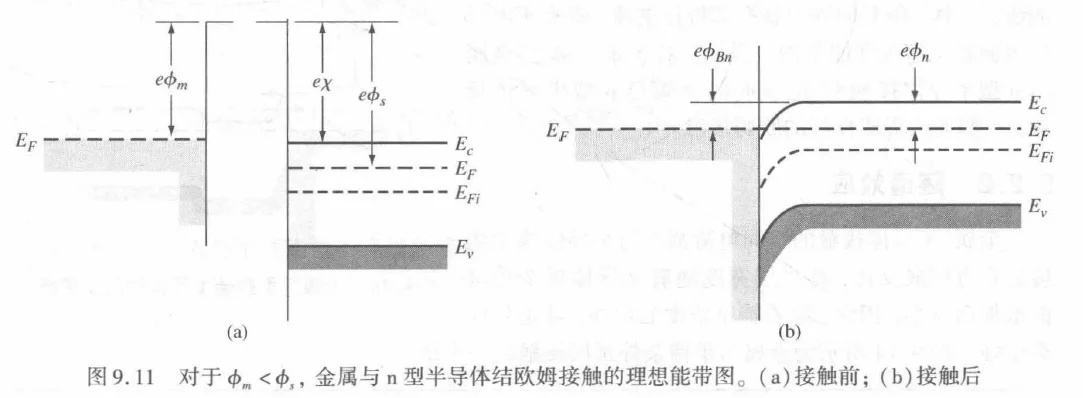
ϕm<ϕs,意味着金属的费米能级高于N型半导体的费米能级:EFm>EFN。
在接触瞬间,为了达到热力学平衡(费米能级拉平),电子从能量较高的金属流向能量较低的半导体。
- 表面状态: 电子流入半导体表面,使得表面处的多数载流子(电子)浓度远高于体内浓度,形成积累层。
| 半导体材料 | N型欧姆接触合金材料 | P型欧姆接触合金材料 |
|---|
| **锗 (Ge)** | 锡、锡锑合金、锡砷合金、铅锑合金、铅锑锡合金、金锑合金 | 铟、铟铅合金、铟镓合金、金镓合金、金锗合金 |
| **硅 (Si)** | 金锑合金、金砷合金、银铅锑合金、镍、铝 | 铝、铝镓合金、铝锡合金、金硼镓合金、镍 |
| **砷化镓 (GaAs)** | 金锡合金、金硒合金、银合金、锡铝合金、铟 | 金锌合金、银锌合金、银铋合金、银锰合金、铟、铟锌合金 |
结场效应晶体管
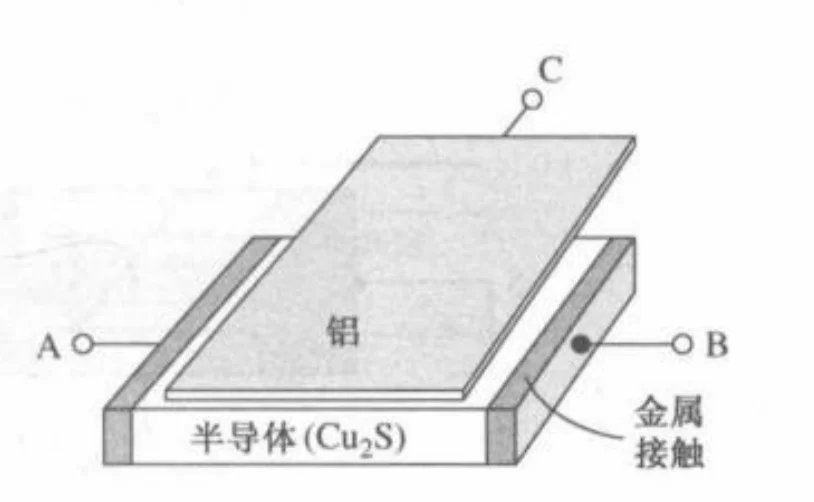
结型晶体管
场效应:半导体电导被垂直于半导体表面的电场调制的现象
多子器件: 与 BJT 利用少子扩散不同,FET主要依靠多数载流子的漂移运动导电。
单极型晶体管: 因为只涉及一种载流子参与导电,故称为单极型。
| 类型 | 说明 |
|---|
| pn结JFET | 利用PN结的反偏耗尽层宽度来调制沟道。 |
| MESFET | 利用金半接触(肖特基接触)来调制沟道。 |
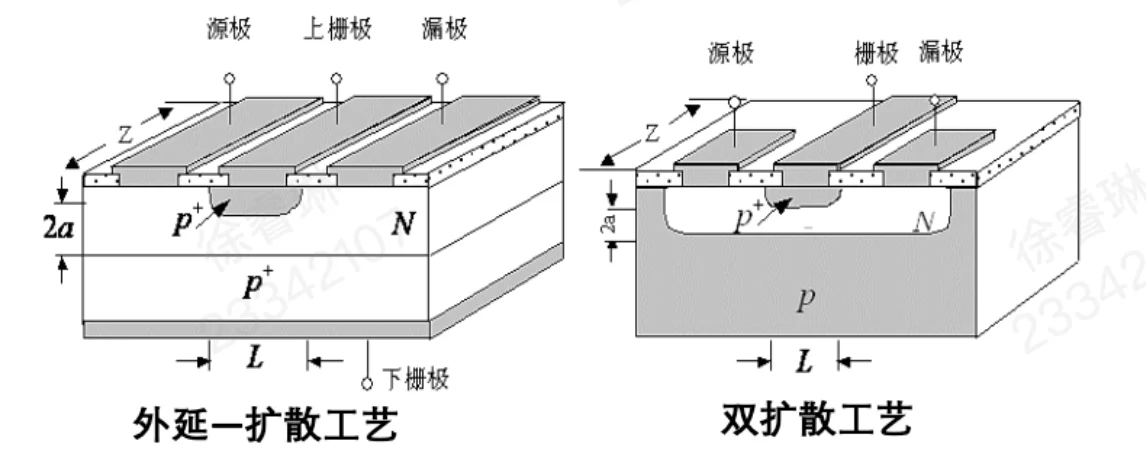
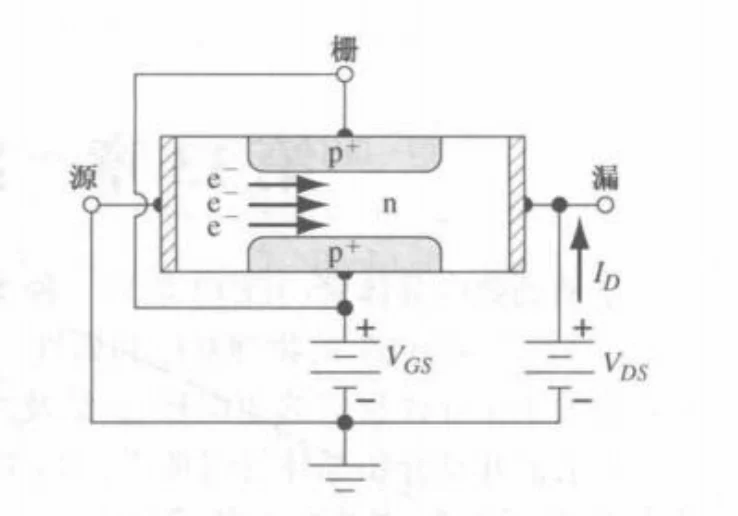
工作沟道示意图
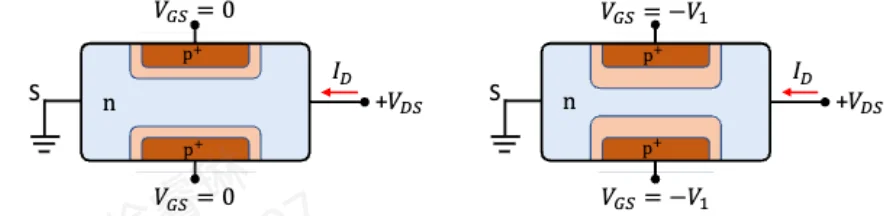
上下两个 P+ 区之间夹着的 N 区构成了电子流通的路径,称为导电沟道。因为沟道(n 型)的多子是电子,所以称为 N 沟道 JFET。
当栅极电压没有关断沟道时,施加漏源电压 VDS。该电压在 N 型沟道内部产生沿轴向的电场。N 区中的多子(电子)在电场作用下,从源极向漏极做漂移运动,形成宏观电流 ID(电流方向定义为与电子运动方向相反,即从 D 流向 S)。
-
施加使 PN 结反向偏置的垂直控制电压 VGS,使 pn 结空间电荷区(耗尽层)变宽。
-
由于 N 区掺杂浓度通常低于 P+ 区,耗尽层主要向 N 型沟道一侧扩展。
-
当施加的电压使得上下两侧的耗尽层在沟道中央相遇时,导电沟道被完全夹断,此时 ID 降为零,晶体管关断。
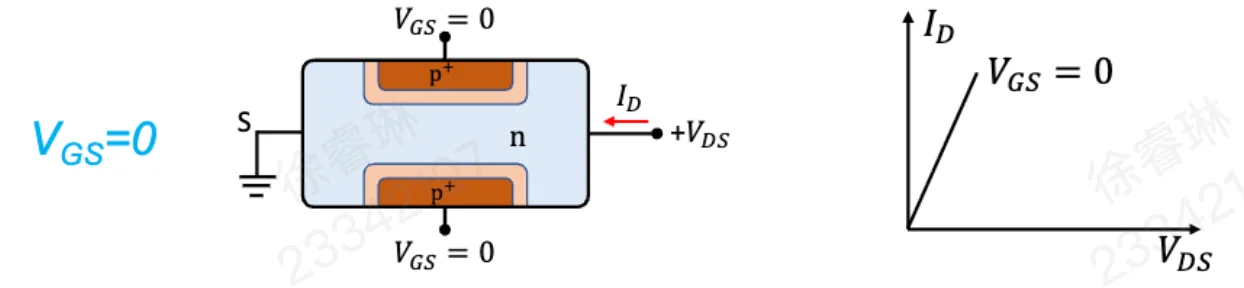
此时沟道电阻最小。ID−VDS 表现为一条斜率较大的线性关系。
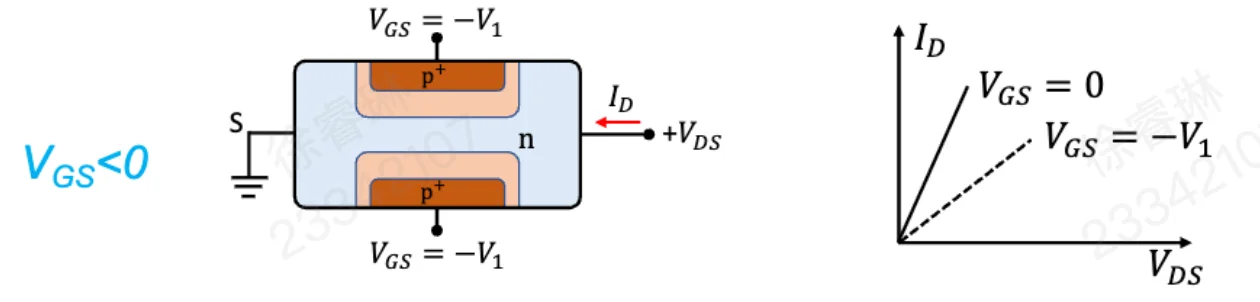
耗尽层向沟道中心扩展,有效导电沟道的截面积减小,反映在图上就是直线的斜率变小。
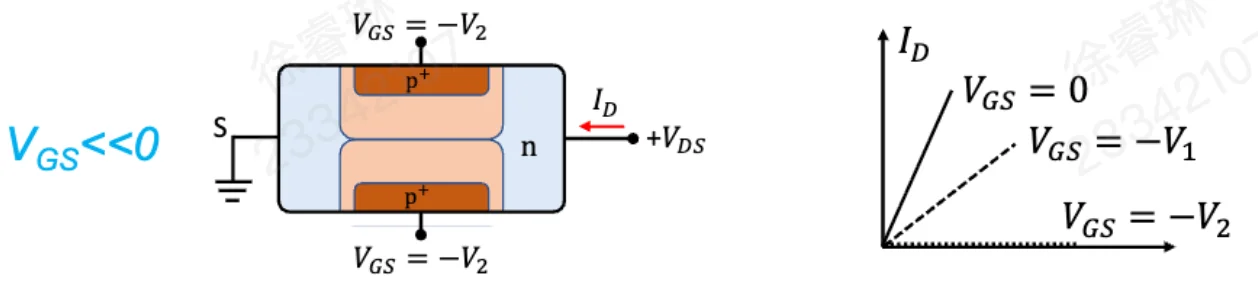
负偏压进一步增大,接近夹断电压。耗尽层占据了绝大部分沟道,剩下的导电通道极窄。ID−VDS 曲线极其平缓,斜率接近于零,电流微弱。
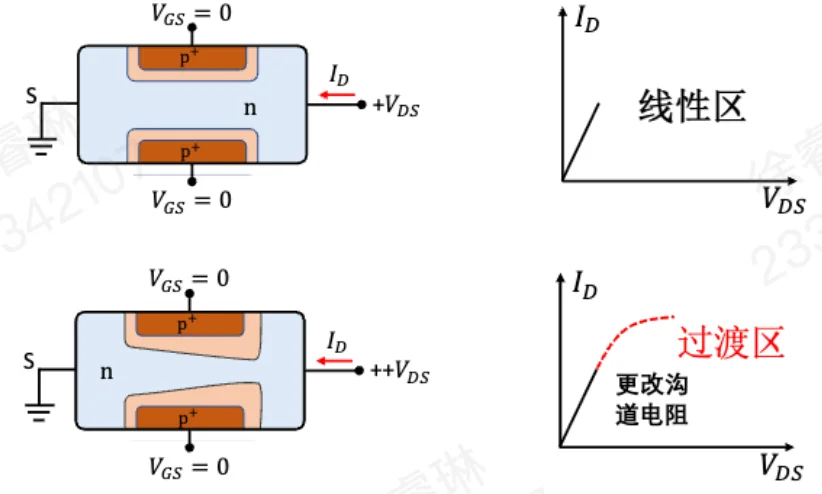
线性&过渡区: 如图可见,随着 VDS 的增大,类似 MOSFET 的沟道夹断机制,因为 N 区的电势高于 P 区的电势,形成 PN 反偏,所以在沟道内部形成了耗尽层,而且越靠近漏端夹断程度越严重。同时也使有效导电沟道的平均截面积减小,使电阻增加,斜率变缓。
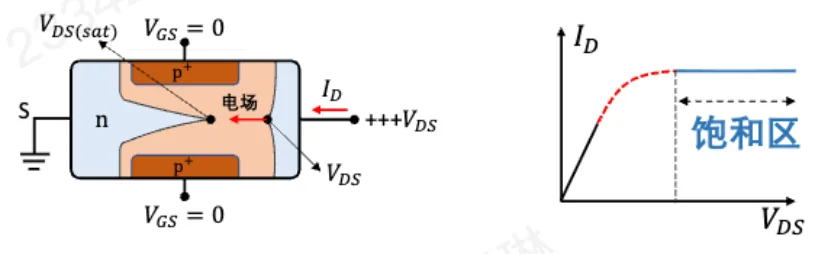
饱和区: 当 VDS≥VDS(sat) 时,漏端的反向偏置电压足以使上下两侧的耗尽层在中心相遇,此时沟道刚好被夹断。
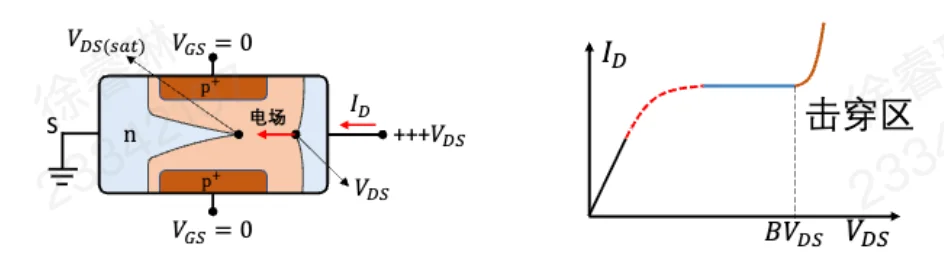
击穿区: VDS>BVDS(漏源击穿电压)
沟道内的初始耗尽层厚度增加。即在未加漏源电压之前,导电沟道的有效横截面积就已经被预收缩了
饱和点偏移: 由于栅极已经提供了一部分反向电压(VGS),漏极只需要提供较小的 VDS 就能使总电压达到夹断条件,即:
VDS(sat,VGS<0)<VDS(sat,VGS=0)
击穿电压降低:击穿主要发生在反偏最强的栅-漏结。击穿条件取决于栅漏两端的总压差 ∣VGD∣=∣VGS−VDS∣=∣VGS∣+VDS。由于 ∣VGS∣ 的存在,只需要较小的 VDS 就会达到雪崩击穿临界场强。因此,VGS 越负,击穿电压 BVDS 越低。
VGS 足够小时,使得上下两侧的耗尽层在沟道中央完全闭合(接触) 时,这个电压值称为夹断电压 VP(或 VGS(off))。
我们仍然分析典型 N 沟道耗尽型 JFET 的输出特性:
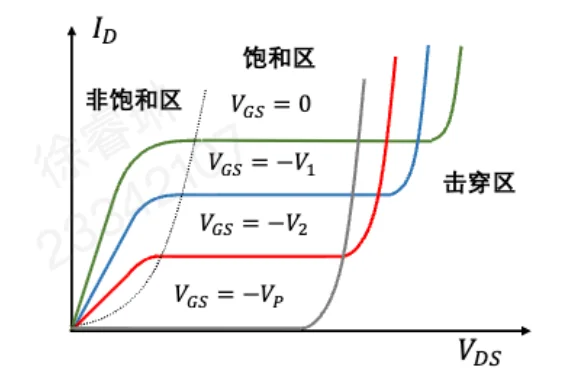
总结起来就一句话:栅结反偏压可改变耗尽层大小,从而控制漏电流大小。 即场效应的精髓
| 对比维度 | JFET | BJT | 解释 |
|---|
| 高频/开关特性 | 优异 | 较差 | JFET是多子器件,无少子存储效应,截止频率fT高,开关速度快。 |
| 输入电阻 | 极高 (约109 Ω) | 较小 | JFET输入端是反偏PN结,反偏电阻极大。易于级间直接耦合,不从信号源抽电流,便于微波系统阻抗匹配。 |
| 抗辐射能力 | 强 | 较弱 | 辐射通过产生晶格缺陷降低少子寿命影响器件,而JFET为多子器件。 |
| 工艺兼容性与材料 | 结构简单,与BJT、MOS工艺兼容。 | 标准硅基工艺成熟 | JFET工艺(外延、扩散)与BJT/MOS兼容,便于集成。 |
| PN-JFET | MESFET |
|---|
| 栅极 | 利用 P+N 结的反向偏置耗尽层控制沟道。 | 直接利用金属-半导体肖特基接触充当栅极。 |
| 原理 | PN结耗尽层随反偏电压变化调制沟道宽度。 | 肖特基结耗尽层随偏压变化控制沟道,类似PN结但为金属-半导体结。 |
| 相比于 PN 结,肖特基结的制作工艺更加简单,而且无需高温扩散过程,有利于保持材料的高迁移率特性。 | | |
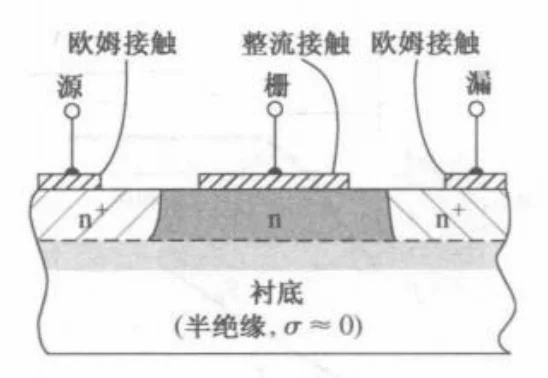
肖特基耗尽层宽度:
W=xn=[eNd2ϵs(Vbi+Va)]1/2
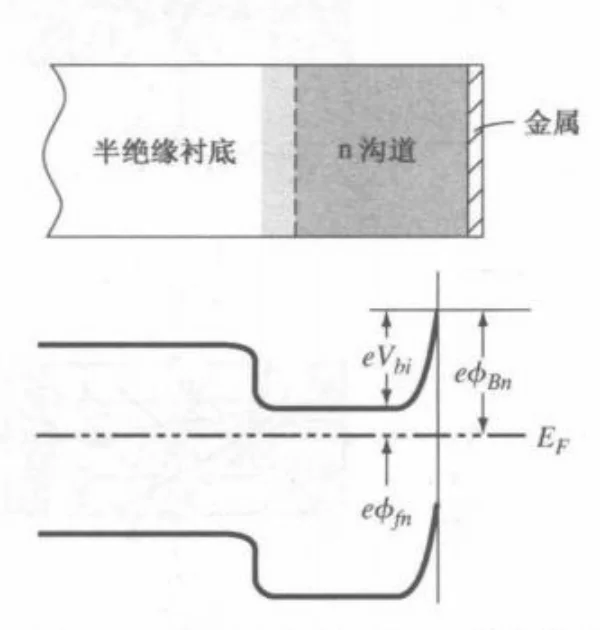
我们一般选用 GaAs 来制作 MESFET的 N 型沟道部分:GaAs 的电子迁移率是 Si 的 5-6 倍。这意味着在相同的几何尺寸下,电子飞越沟道的速度更快,器件的工作频率更高(适合微波/射频应用)。而且也可以生长在半绝缘衬底上,减小期间的
和增强型 BJT 原理相同,在控制电压为 0时,已经关断了沟道,需要施加正向栅压来打开沟道。
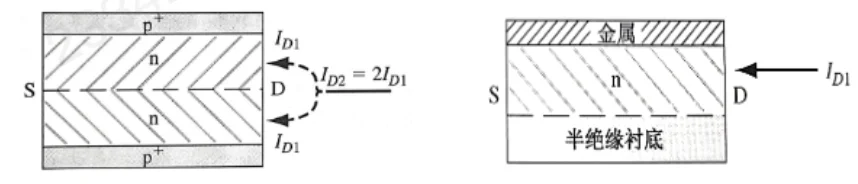
传统的 JFET 结构是上下两个 p+ 区夹着中间的 n 沟道。为了简化分析,我们可以将这种双边器件看作是==两个单边器件的并联==。
后续我们将分析双边结的器件特性。
由于结构的对称性,双边器件的总漏极电流 ID 等于单边电流的 2 倍:
ID=ID2=2ID1
基于单边突变结近似,我们可推导反偏条件下(VGS<0)耗尽层宽度 h 的表达式:
h=[eNd2ϵs(Vbi−VGS)]1/2
设沟道的半宽度为 a(即从中心到冶金结边界的距离)临界条件即当耗尽层宽度 h 扩展到等于沟道半宽度 a 时,导电沟道被完全夹断。
将 h=a 代入上述公式,反解出夹断电压 VP0,即==临界条件下(Vbi−VGS) 的表达式==:
VP0=2ϵsea2Nd
| 参数 | 符号 | 物理意义 | 说明 |
|---|
| 内建夹断电压 | VP0 | 沟道(假设VGS=0)内部耗尽所需的总电势差。 | 由半导体掺杂浓度ND、介电常数εs、沟道厚度a等本征参数决定,例如对均匀掺杂N沟道:VP0=2εsqNDa2 |
| 夹断电压 | VP | 为耗尽沟道,需要在栅源端口外部施加的电压。 | 在VGS=VP时,沟道被完全夹断。通常VP=Vbi−VP0,其中Vbi为内建电势。 |
Vbi−VP=VP0
对于通常的耗尽型 JFET,要实现沟道夹断,所需的总电势 VP0 通常大于内建电势 Vbi。因此,VP=Vbi−VP0<0。
即 N 沟道耗尽型 JFET 的夹断电压(阈电压)是一个负值。
约束条件:
内建夹断电压 VP0: 依然定义为耗尽 a 宽度所需的总电势:
VP0=2ϵsea2Na
电压关系:
Vbi+VP=VP0⇒VP=VP0−Vbi
当我们施加了漏源电压之后,
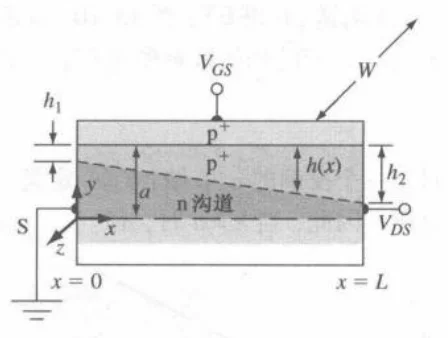
h1=[eNa2ϵs(Vbi−VGS)]1/2h2=[eNa2ϵs(VDS+Vbi−VGS)]1/2
显然 h2>h1,这验证了沟道在漏端最窄的结论,当漏端耗尽层宽度 h2 增加到等于沟道半宽度 a 时,发生夹断。
此时漏端的总反偏电压为 Vbi+VDS(sat)−VGS,即:
Vbi+VDS(sat)−VGS=Vp0
| 器件类型 | 饱和电压公式 |
|---|
| n 沟道 | VDS(sat)=Vp0−(Vbi−VGS) |
| p 沟道 | VDS(sat)=Vp0−(Vbi+VGS) |
我们取沟道中坐标为 x 处、长度为 dx 的一小段微元。其电阻由电阻定律决定:
dR=A(x)ρdx=σA(x)dx
由 σ=eμnNd(N沟道),且 A(x)(有效沟道面积)由于是单边模型,截面积为宽度 W 乘以有效高度 [a−h(x)]。
代入微分电阻公式:
dR=eμnNd[a−h(x)]Wdx
由:
dV(x)=ID1dR
将 dR 的表达式代入并整理,得到关于 x 和 V 的微分方程:
ID1dx=eμnNdW[a−h(x)]dV(x)
由:
h(x)=[eNd2ϵs(Vbi+V(x)−VGS)]1/2
对上式两边微分,可以将电压微分 dV(x) 转化为耗尽层宽度微分 dh(x) 的表达式:
dV(x)=ϵseNdh(x)dh(x)
将 dV(x) 代回原微分方程,消去电压项,得到纯粹关于 h(x) 的积分式:
ID1dx=ϵsμn(eNd)2W[a−h(x)]h(x)dh(x)
积分运算 ∫(ah−h2)dh=2ah2−31h3,得到电流 ID1 的初步表达式:
ID1L=ϵsμn(eNd)2W[2a(h22−h12)−31(h23−h13)]
为简化公式,我们定义夹断电流 IP1:
IP1=6ϵsLμn(eNd)2Wa3
物理意义:栅极零偏(VGS=0)且内建电势可以忽略(或 Vbi=0)时的理论最大漏极电流。反映了器件导电能力的上限。
将所有需要代入的量(h1 和 h2,Vp0 和 IP1)代入漏源电流公式进行化简:
ID1=IP1[3Vp0VDS−2(Vp0VDS+Vbi−VGS)3/2+2(Vp0Vbi−VGS)3/2]
沟道电导 gd 定义为:
gd=∂VDS∂ID1VDS→0
代入漏源电流公式:
gd=Vp03IP1[1−(Vp0Vbi−VGS)1/2]
观察可得最大电导 G01:
G01=Vp03IP1
物理意义: 这是当栅压为零(VGS=0)且忽略内建电势(Vbi=0)时的理想最大沟道电导,和刚才的理想最大电流匹配。
当 VDS 达到饱和电压时,即 VDS=VDS(sat)=Vp0−(Vbi−VGS),代入方程:
ID1(sat)=IP1[1−3Vp0(Vbi−VGS)(1−32Vp0Vbi−VGS)]
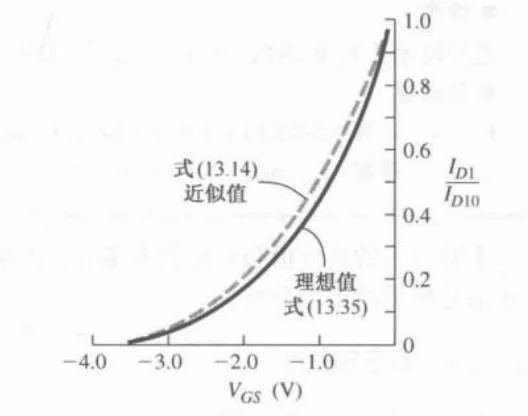
理论公式(含有 3/2 次方项)过于复杂,不便于电路设计和手算估算,工业界常采用一个简化的二次函数来拟合饱和漏电流:
IDsat=IDSS(1−VPVGS)2
跨导 gm 描述了==栅源电压 VGS 对漏极电流 ID 的控制能力==:
gm=∂VGS∂IDVDS=const
对通用电流方程关于 VGS 求偏导,得到中间公式:
gmL=Vp03IP1Vp0Vbi−VGS(Vbi−VGSVDS+1−1)
使用泰勒展开化简:
gmL≈2G01Vp0(Vbi−VGS)VDS
在线性区,跨导 gmL 与漏源电压 VDS 成正比。这意味着在线性区,VDS 越小,栅极对电流的控制能力越弱。
对饱和电流方程 ID1(sat) 关于 VGS 求导,得到:
gms=∂VGS∂ID1(sat)=G01(1−Vp0Vbi−VGS)
使用工业平方律电流公式进行化简:
gms=−VP2IDSS(1−VPVGS)
对于 N 沟道 JFET,VP 是负值,因此系数 −VP2IDSS 是正值,保证了跨导 gms 为正值(即 VGS 增加,电流 ID 增加)。
我们在这里只关注 n 沟道 GaAs MESFET 的特性,除了结的构成不同,其余 I/V 特性基本与 pn JFET 相同(底层物理机制相同)。
阈值电压:
VT=Vbi−VP0
要制备增强型(即要求 Vbi>VP0),必须减小 VP0。根据 VP0=2ϵsea2Nd,因此可以从两个工艺手段下手:
-
薄的沟道厚度(a)**。
-
低沟道掺杂浓度(Nd)**。
这样可以显著降低 VP0,使其小于内建电势 Vbi,从而实现“常关”特性。
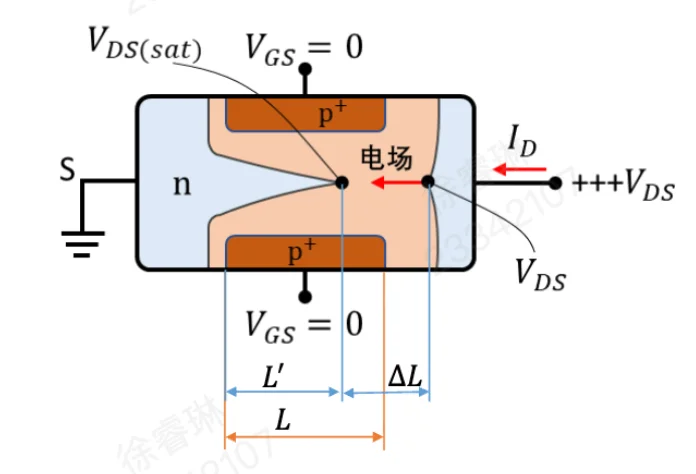
当 VDS 继续增加超过饱和电压时,漏端的反向偏置电压进一步增大。这导致漏端附近的耗尽层不仅在垂直方向上夹断,还在水平方向(沿沟道方向) 向源极延伸。
有效沟道长度 L′:
L′≈L−2ΔLΔL≈[eNd2εs(VDS−VDS(sat))]1/2
根据电阻定律,沟道电阻与长度成正比。因此,电流与沟道长度成反比。
修正后的电流 ID1′ 与原理想电流 ID1 的关系为:
ID1′=ID1×L−2ΔLL
为了方便计算,通常引入一个修正因子 (1+λVDS),得到修正后的饱和电流方程:
ID1(sat)′=ID1(sat)(1+λVDS)
输出阻抗(rds):
rds=∂ID1′∂VDS≈ΔID1′ΔVDS
由于夹断后电流随电压略有增加(而非理想的零增加),JFET 在饱和区的输出阻抗 rds 是有限的(而非理想的无穷大)。
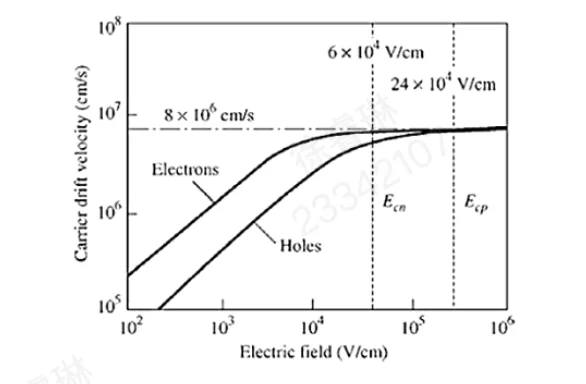
当电场达到临界值 Ecn 或 Ecp 时,载流子速度达到极限值 vsat(约为 107cm/s 数量级),此后不再随电场增加。
发生条件: 在沟道较短或偏置电压较高时,沟道漏端的电场可能在沟道尚未几何夹断之前,就已经大到使载流子速度达到 vsat。
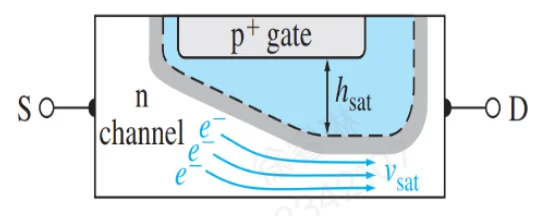
ID1(sat)=eNdvsat(a−hsat)W
- hsat:达到速度饱和时的耗尽层宽度。





























