数据通路

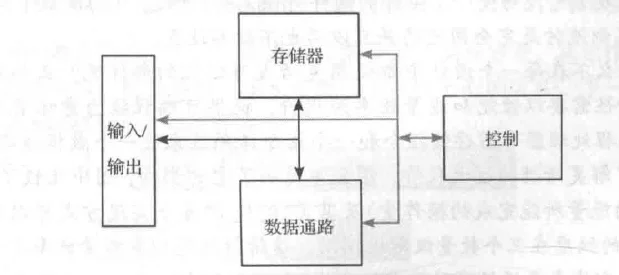
一般数字处理器的组成

首先需要建立设计复杂算术逻辑单元（ALU）或处理器数据通路时的方法论基础。在设计像加法器这样的复杂电路时，我们遵循以下核心原则：

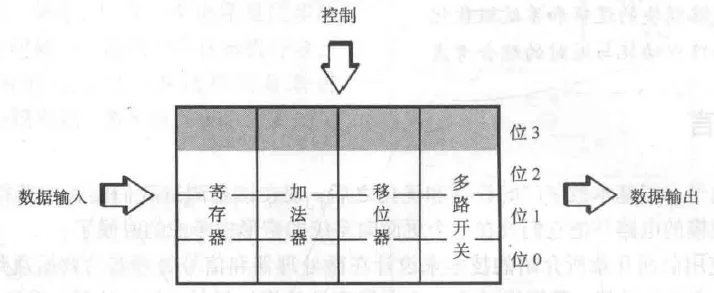
位片式数据通路结构

1. 规整性 & 位片式实现：

为了处理$N$位的数据，我们不需要设计$N$种不同的电路，而是设计一个标准位片单元，然后将其复制$N$次。

位片就是一个能够独立处理单位长度数据（可以是字节，字，也可能是比特）的完整功能模块（如xx位全加器，xx位寄存器，多路选择器等）。而位片式结构就是很多处理单位长度的数据的模块的叠加。

2. 局域性：

   • 指信号的交互主要发生在相邻的位片之间或模块内部。

运算往往是顺序执行或级联的。相邻连接体现了局域性，有利于减少长线互连带来的寄生效应和延迟。

3. 正交性：

   • 指 控制流 与 数据流 在几何结构和逻辑上的解耦。

4. 层次化：

   • 设计是分层进行的。从高位到低位，或从多位宽模块分解为少位宽模块。不同层次可以采用不同的物理实现方式，以平衡面积和速度。

5. 模块化：

   • 将功能封装为IP模块（如加法器、乘法器）。这使得设计可以像搭积木一样复用成熟的子电路。

加法器设计

加法是最常用的运算操作，也常常是限制处理器速度的元件。

结构	逻辑级数	最大扇出	布线通道	单元数
Carry-Ripple	$N-1$	1	1	$N$
Carry-bypass (4段)	$\frac{N}{4} + 5$	2	1	$1.25N$
平方根进位选择	$\sqrt{2N}$	$\sqrt{2N}$	1	$2N$
Brent-Kung	$2\log_{2}N - 2$	2	1	$2N$
Sklansky	$\log_{2}N$	$\frac{N}{2} + 1$	1	$0.5N\log_{2}N$
Kogge-Stone	$\log_{2}N$	2	$\frac{N}{2}$	$N\log_{2}N$

二进制加法器概述

基本单元

• 半加器：仅考虑两个本位输入 $A$、$B$，不考虑低位进位（也就是全加器的式子里把 $C_i$ 全置为0）。由一个XOR门（产生Sum）和一个AND门（产生Carry）组成。

• 全加器：多位加法的基础，须处理三个输入：本位操作数 $A$、$B$ 以及来自低位的进位输入 $C_{in}$。输出为本位和 $Sum$ 及向高位的进位输出 $C_{out}$。

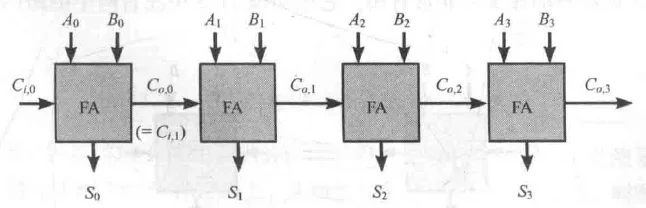
最基本的 — 逐位进位加法器

基本逻辑方程

$$\begin{aligned} S &= A \oplus B \oplus C_i \\\\ &= A\bar{B}\bar{C}_i + \bar{A}B\bar{C}_i + \bar{A}\bar{B}C_i + ABC_i \\\\ C_o &= AB + BC_i + AC_i\\\\ &= AB + C_{in}(A+B) \end{aligned}$$

全加器真值表

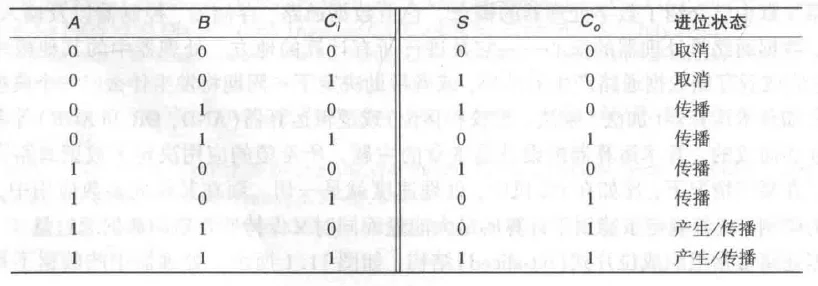
高速加法器基础：

类型	达成条件	$C_o$ 表达式	说明
Delete（进位消除）	$A=0,\; B=0$	$C_o = 0$	低位的进位 $C_{in}$ 传到这一级会被消除，无论 $C_{in}$ 是什么，$C_{out}$ 恒为0
Propagate（进位传播）	$A \neq B$	$C_o = C_{in}$	当 $A$ 与 $B$ 取值相异时，低位进位信号直接传播穿过这一级，$C_{out} = C_{in}$，同时影响本级和下一级运算
Generate（进位产生）	$A=1,\; B=1$	$C_o = 1$	该位主动产生一个新的进位信号向高位发送，无论 $C_{in}$ 是什么，$C_{out}$ 恒为1

行波进位加法器

第 $i$ 位的最终结果不仅取决于 $A_i, B_i$，还隐含地取决于 $A_{i-1}...A_0$ 和 $B_{i-1}...B_0$。

进位链：最高位的 $C_{out}$ 必须==等待最低位的 $C_{in}$ 经过所有中间位的处理==后才能确定。

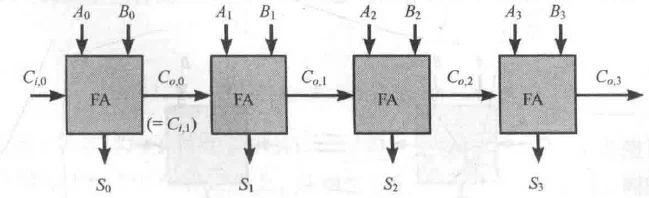
行波进位加法器

时序延迟

延迟时间公式：

$$t_{adder} = (N-1)t_{carry} + t_{sum}$$

最坏情况的延时与加数位数 N 成线性关系，即时间复杂度：$t_d = O(N)$。

意味着如果我们把位数翻倍，运算延迟将也增加一倍。在高速计算中是不可接受的瓶颈，因此设计的关键在于加快进位信号传播的速度。

进位信号的抽象重构

进位产生、进位取消、进位传播信号

类型	逻辑表达式
G	$G = AB$
K/D	$K = \overline{A}\overline{B}$
P	$P = A \oplus B$

加法逻辑表达式重构

• $S(G, P) = P \oplus C_i = (A \oplus B) \oplus C_i$

• $C_o(G, P) = G + PC_i$

全加器的反向特性

标准的CMOS逻辑门（NAND, NOR）输出天然是反相的。要得到正逻辑（AND, OR），通常需要级联一个反相器。这会增加延时。

$$\overline{S}(A, B, C_i) = S(\overline{A}, \overline{B}, \overline{C}_i)$$ $$\overline{C}_o(A, B, C_i) = C_o(\overline{A}, \overline{B}, \overline{C}_i)$$

如果将全加器的所有输入 ($A, B, C_{in}$) 都取反，那么输出 ($S, C_{out}$) 也会自动变成原来输出的反码。此特性允许我们在处理反相信号时，不需要通过反相器将其恢复为正信号再运算，而是直接用反相信号进行运算，得到反相的结果。

单级全加器设计及优化

经典静态互补设计

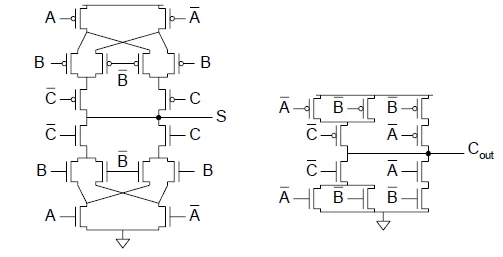
如果直接分别使用两套电路计算求和结果以及进位结果，晶体管统计：

项目		数量
S	$S = A \oplus B \oplus C_{i} = ABC_{i} + \overline{A}B\overline{C}_{i} + \overline{A}BC_{i} + \overline{A}\overline{B}\overline{C}_{i}$	需 16 个管子
$C_o$	$C_{o} = AB + C_{i}(A + B)$	需 10 个管子
反相器	3 个	需 6 个管子
总共		36个管子

记住这两个电路，非常经典。

无XOR复合门实现方案

利用 $Carry-out$ 信号产生 $Sum$，省去了庞大的XOR门结构，总管子数降为28个：

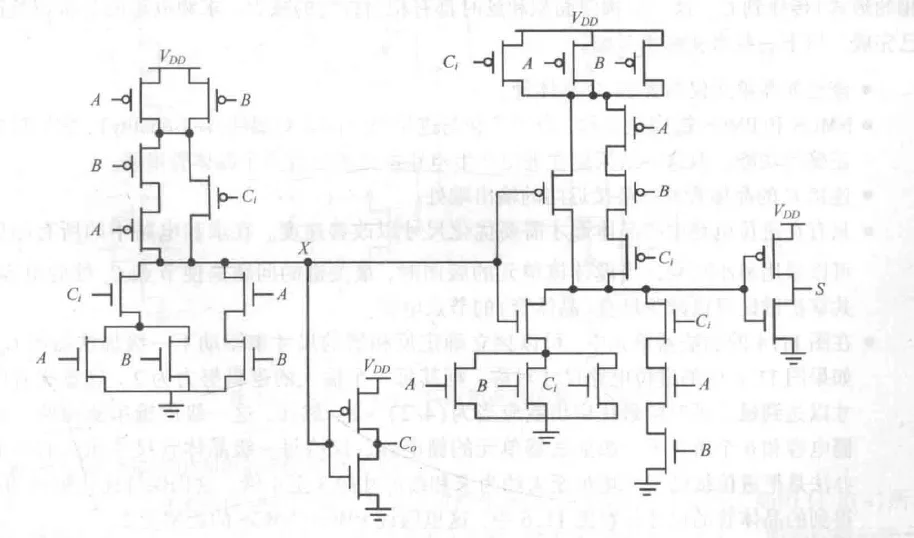
互补静态全加器实现电路（进位电路复用）

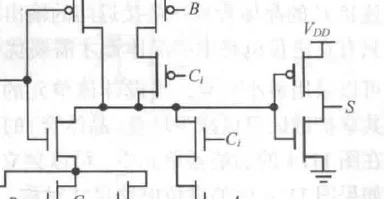
在本电路中，设计者利用了 $C_{out}$ 信号来辅助生成 $Sum$：

$$C_o = AB + BC_i + AC_i$$ $$S = ABC_i + \overline{C_o}(A+B+C_i)$$

由于$Sum$ 是由 $C_{out}$ 推导出来的，所以 $Sum$ 的生成肯定晚于 $C_{out}$，但在行波进位加法器中，关键路径是进位链。只要 $C_{out}$ 够快，$Sum$ 稍微慢一点是可以接受的（高位的 $Sum$ 反正要等低位的 $C_{out}$）。

劣势：

节点电容负载超大导致时间常数增大，让充放电时间变长，导致进位信号传播变慢。

负载组成：

1. 本级负载：进位输出反相器的源漏扩散电容。

2. 内部耦合：因为 $Sum$ 的生成依赖 $C_o$，所以 $C_o$ 还要驱动本级内部产生 $Sum$ 的电路。

3. 下一级负载：驱动下一级全加器的6个栅电容 (数一下一级全加器正好是六个$C_i$的输入端) 以及级间连线的布线电容 。

消除输出反相器的行波进位加法器

目的：

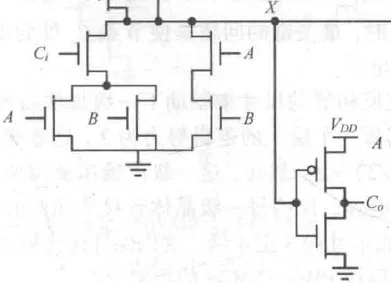
之前的进位/求和结果输出是带反相器的

这两个反相器会或多或少影响延时，因此可以利用全加器的反相特性来减免这两个延时（主要是减少进位链的延时，求和结果减不减无所谓）。

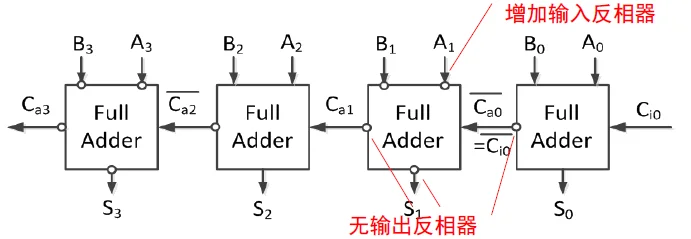
消除输出反相器的行波进位加法器

0级全加器直接去除进位反相器，1 级的全加器把输入也变成反的，由于取消了输出反相器，所以全加器把进位信号再次取反，回到了正的进位信号。如此奇偶交替则逻辑正确，速度也变快了。

镜像加法器

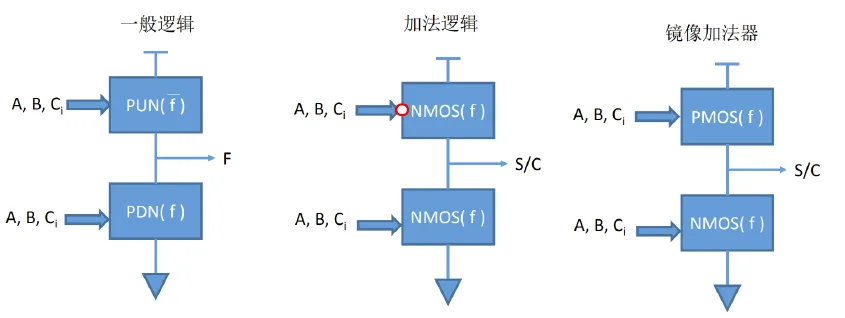
镜像电路演变过程

一般的静态互补逻辑如左图所示，上下需要设计不同的拓扑电路结构以满足同输入下拥有正好相反的导通结果，但是加法逻辑不一样，只需要把输入反过来（即输入添加一个反相器），就可以让一个拓扑电路结构重复使用。

然而正好 PMOS 和 NMOS 的导通逻辑相反，所以直接反相器也不用加了，直接 PMOS 和 NMOS 镜像结构就能实现加法逻辑，当然，这个情况仅限于拥有反相特性的加法逻辑。

最后把管子数优化到 24 个。

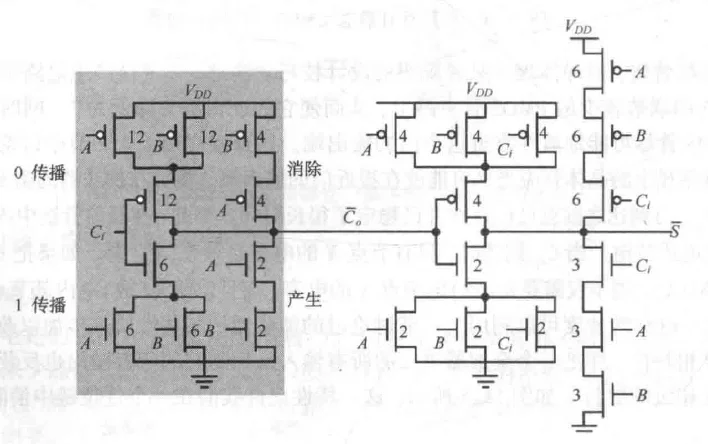
镜像加法器电路图

记住这个电路，也很重要。

传输门加法器

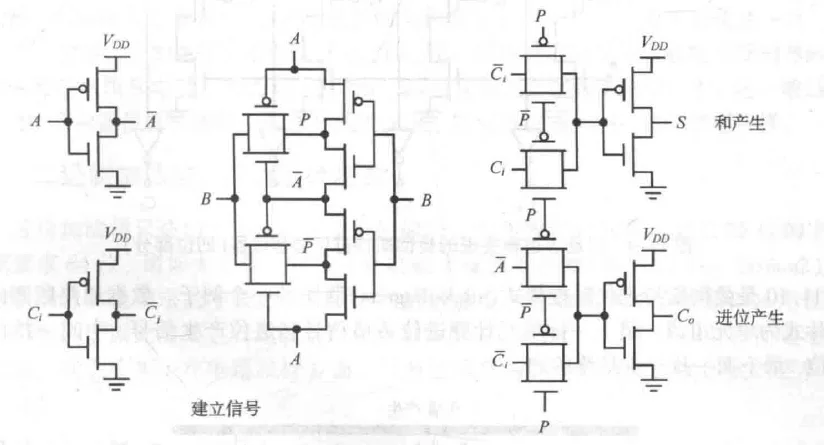
传输门加法器电路图

P set-up 电路的左半边不是很理解，$P$ 和 $\overline{P}$ 都会多加一份没必要的逻辑？

特点：

• 24个晶体管：与镜像加法器数量持平，具有较高的面积效率。

• 时序对称性：$SUM$ 和 $Carry$ 的延时时间相同，从结构来看也是高度对称的。

高速进位链设计

曼彻斯特进位门

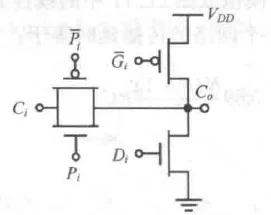
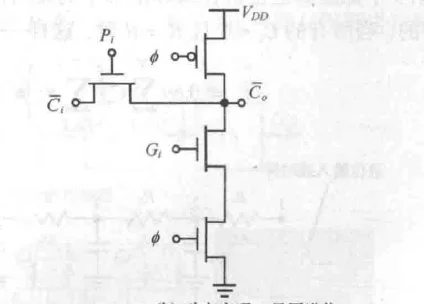
静态、动态曼彻斯特进位门

彻底利用抽象的进位标志来传播进位，而且使用了传输门逻辑，电路还是好理解的，而且加法逻辑的互斥性保证两个进位标志不会同时为 1，防止充放电冲突。

曼彻斯特进位链

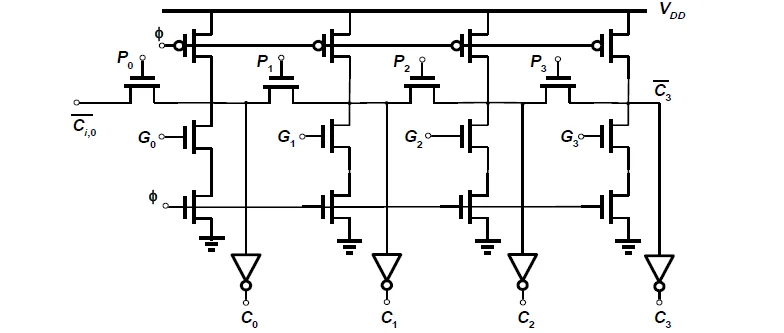
曼彻斯特进位链

曼彻斯特进位链呈现出多米诺风格的级联结构。

进位链传输管只用N管，节点电容很小，为四个扩散电容。

根据Elmore延时模型，$N$级曼彻斯特进位链的延时：

$$t_{p}=0.69\sum_{i=1}^{N} C_{i}\left(\sum_{j=1}^{i} R_{j}\right)=0.69\frac{N(N+1)}{2} RC$$

进位选择加法器

概述

注意这是加法块之间的进位传递优化，针对的加法数据也是大位宽的数据。

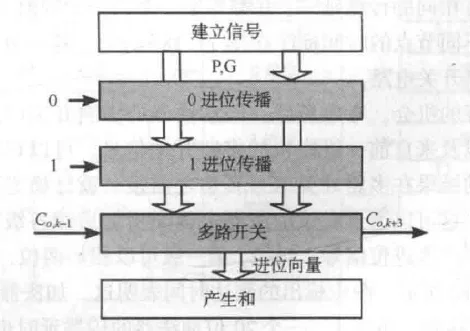
进位选择加法器设计蓝图

动机： 在传统的行波进位加法器中，第 $k$ 级（假设分为4位一级）必须等待第 $k-1$ 级的进位输出 $C_{o, k-1}$ 到达后才能开始有效计算。为了打破这种等待，我们采用预测的方法（有点像微机原理的分支预测），硬件开销增加了约30%。

双路径并行计算

由于输入进位 $C_{in}$ 只有两种可能性（“0”或“1”），对于每一位的加法，两条独立的进位传播路径：

• “0” 进位传递：假设本级进位输入为 0，预先计算出一套结果（和与进位输出）。

• “1” 进位传递：假设本级进位输入为 1，预先计算出另一套结果。

• 设置电路：用于生成所有位所需的 $P$ 和 $G$ 信号，供上述两条路径使用。

进位选择是分块双路而非全局裂变：每一块只需为当前的 $C_{in}$（0或1）准备两套剧本，前级送来的进位只是一个负责二选一的‘开关’，它在每一级末尾都把状态收敛回了‘1’，所以没有引爆指数级。

每一级使用一个 $MUX2$ 选择剧情走向即可。

线性进位选择加法器

关键路径分析

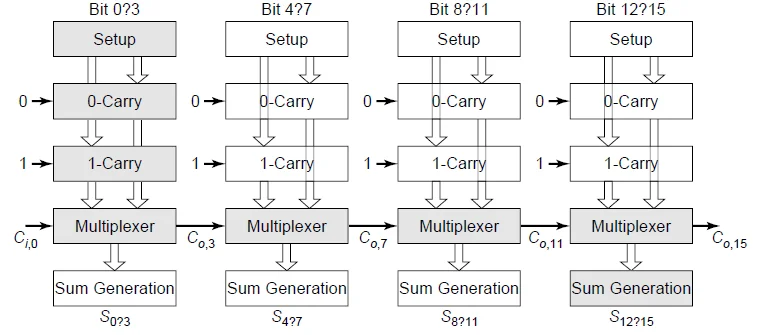
如图一共是计算 16 位数（即总位数 $N$ ）的运算，分成 4 块 4 位（即分块位数 $M$ ）的加法。

$$t_{\text{add}} = t_{\text{setup}} + M t_{\text{carry}} + \left(\frac{N}{M}\right) t_{\text{mux}} + t_{\text{sum}}$$

• 解释： 总时间 = 准备时间（所有块一起准备，所以算作1个） + M 个 块内进位传递时间（块内是线性）+$\frac{N}{M}$ 个选择器时间 + 最后的求和时间

对比传统行波加法器的 $O(N)$ 延迟，这里虽然项中仍含有 $N$，==但 $t_{mux}$ 通常远小于 $t_{carry}$，因此速度有显著提升==。

信号时间分配不均衡

在线性进位选择加法器中，我们将 $N$ 位加法器划分为固定长度（例如均为 $M=4$ 位）的块。

每个块内部的两条进位链是并行计算的。内部计算在 $t_{setup} + M \cdot t_{carry}$ 时刻就已经完成了。

进位链的结果在多路开关信号到达之前很久就已经稳定下来。因此使这两条路径的延时相等是有意义的。

平方根进位选择加法器

既然高位模块必须等待更久的 MUX 信号，那么不妨让高位模块承担更多的计算任务（处理更多位数，比如每高一级就多算一位）。

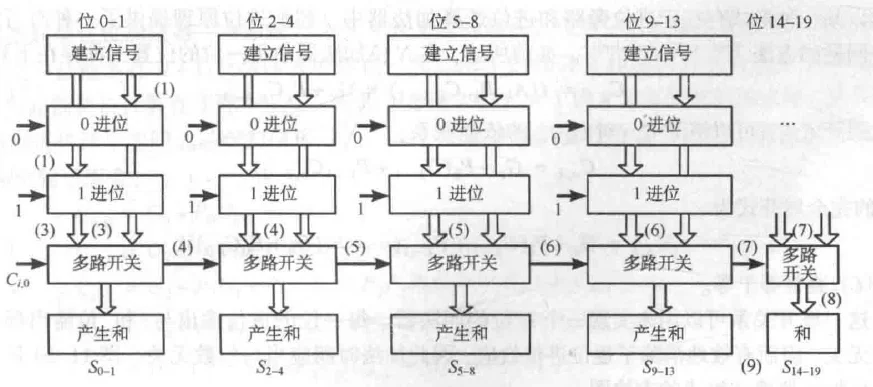
平方根进位加法选择器

于是总位数 $N$ 变成了一个等差数列求和：

$$N = M + (M+1) + ... + (M+P-1)$$

经求和公式推导，得出近似关系：==如果 $N$ 很大，$P \approx \sqrt{2N}$。（P 就是MUX链的长度，也就是级数）==

因此，总延时表达式修正为：

$$t_{add} = t_{setup} + M t_{carry} + \sqrt{2N} t_{mux} + t_{sum}$$

此时延时正比于 $\sqrt{2N}$ (亚线性关系)，而不是 $N$ (线性关系)，当 $N$ 很大时，延时几乎变为常数

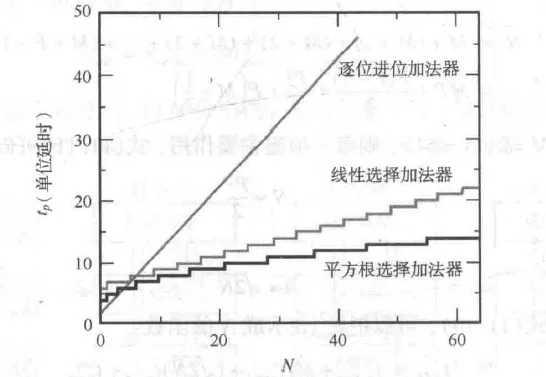
进位选择的优势

进位旁路加法器

相比于标准的行波进位加法器，只是在电路末端增加了一个MUX（硬件开销多了20%）。它的作用是决定最终输出的进位 $C_{o,3}$ 是来自行波进位链的末端，还是直接来自输入进位 $C_{i,0}$。

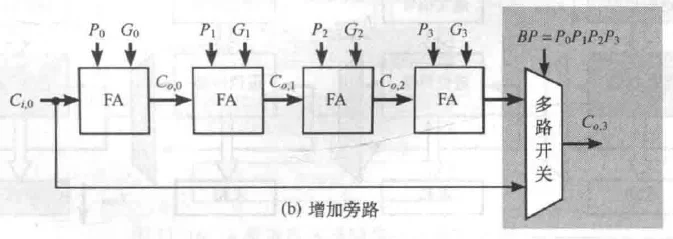
定义 $BP$ 为该块内所有进位传播信号的“与”逻辑，即

$$BP = P_0 P_1 P_2 P_3$$

最坏情况分析：如果是 $BP=0$ 的情况（不能旁路或者差一位就旁路），或者虽然 $BP=1$ 但旁路路径延迟大于行波路径（在小位宽时可能发生），那么关键路径依然是传统的行波进位。此设计旨在优化超长距离进位传播。

关键路径分析

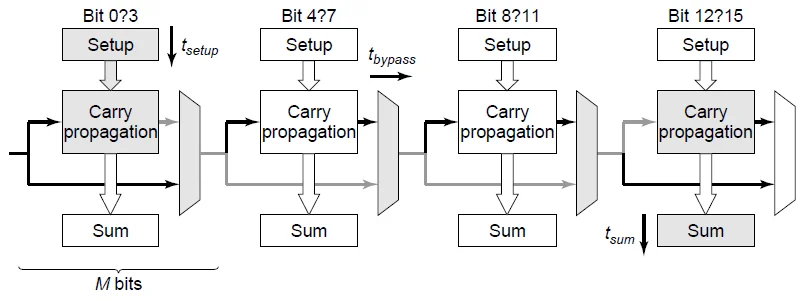
分块的进位旁路加法器

$N$ 位加法器被分成 $N/M$ 个组，每组 $M$ 位。

总延时公式：

$$t_{adder} = t_{setup} + M t_{carry} + (N/M - 1) t_{bypass} + (M-1) t_{carry} + t_{sum}$$

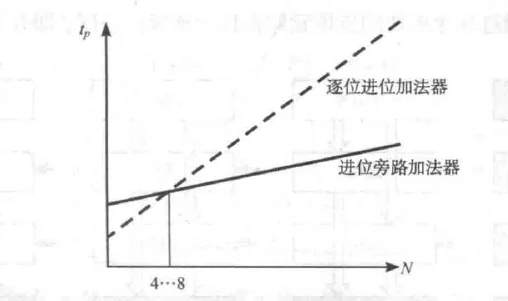
进位旁路加法器的优势 — 适合长距离，位数越大越好

一般N 在4~8 之间采用旁路进位。

超前进位加法器

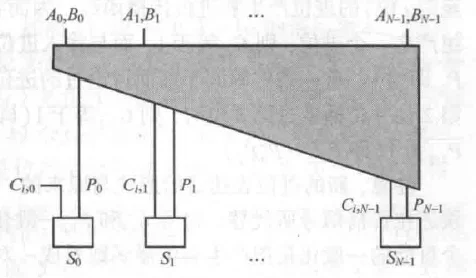
超前进位加法器原理图

每一位的进位输出只与最初的进位输入有关，而与比它低位的其他进位输入无关：

$C_{o,k}=G_{k}+P_{k}C_{o,k-1}$

展开：

$C_{o,k}=G_{k}+P_{k}\left(G_{k-1}+P_{k-1}\left(\ldots+P_{1}\left(G_{0}+P_{0}C_{i,0}\right)\right)\ldots\right)$

$=G_{k}+P_{k}\left(G_{k-1}+P_{k-1}\left(\ldots\left(G_{1}+P_{1}G_{0}\right)\ldots\right)\right)+P_{k}\ldots P_{1}P_{0}C_{i,0}$

可见，进位输出的运算可以变成递归链，一直递归到最底层的输入进位 $C_{i,0}$。

$S_{k}=P_{k}\oplus C_{o,k-1}$
理论上，第1位和第32位的进位是同时计算出来的（理想化的 $O(1)$ 时间复杂度结论，实际的延时至少随位数线性增加）

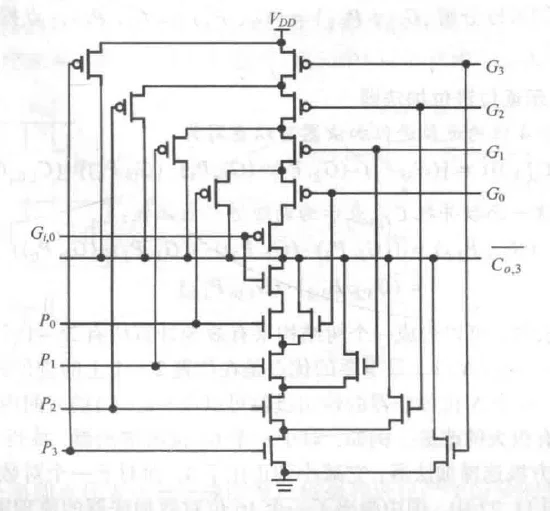
镜像-4位超前进位加法器

缺陷

• 大扇入导致速度变慢：

  • 图中最左侧的NMOS支路是5个晶体管串联。串联的晶体管越多，等效电阻 $R_{on}$ 越大，同时内部节点电容增加，导致放电时间 $\tau = RC$ 急剧增加。

• 大扇出导致延时加大：

  • 最低位的信号（如 $G_0, P_0, C_{i,0}$）参与了所有高位进位的计算。意味着 $P_0$ 信号源需要同时驱动第1位、第2位……直到第N位的进位生成电路。驱动的负载电容（栅电容）巨大。

  • 为了驱动这么大的负载，信号源必须非常强，或者插入巨大的缓冲器，这本身就会带来巨大的延时。

• 面积膨胀：

  • 实现 $N$ 位CLA所需的晶体管数量并不是随 $N$ 线性增长的，而是接近几何级数或平方级增长。对于大位宽，其版图面积将变得不可接受。

树形加法器

似乎是选修章节，暂且不整理这部分的笔记了。