二进制乘法器

乘法运算解构

无符号数乘法

$$\begin{array}{ccccccccc} & & & 1 & 0 & 1 & 0 & 1 & 0 \\ \times & & & & & 1 & 0 & 1 & 1 \\ \hline & & & 1 & 0 & 1 & 0 & 1 & 0 \\ & & 1 & 0 & 1 & 0 & 1 & 0 & \\ & 0 & 0 & 0 & 0 & 0 & 0 & & \\ + 1 & 0 & 1 & 0 & 1 & 0 & & & & \\ \hline 1 & 1 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & \\ \end{array}$$ $$M \text{位} (X=\sum_{i=0}^{M-1} X_i 2^{i}) \times N \text{位} (Y=\sum_{j=0}^{N-1} Y_j 2^{j})$$

结果（将 Z 展开为 X 和 Y 的乘积形式）：

$$Z=X \times Y=\sum_{k=0}^{M+N-1} Z_k 2^{k} = \left(\sum_{i=0}^{M-1} X_i 2^{i}\right)\left(\sum_{j=0}^{N-1} Y_j 2^{j}\right)$$ $$=\sum_{i=0}^{M-1}\left(\sum_{j=0}^{N-1} X_i Y_j 2^{i+j}\right) =\sum_{i=0}^{M-1}\sum_{j=0}^{N-1}(X_{i}Y_{j})\cdot 2^{i+j}$$

我们可以构建一个M行N列的位积矩阵（这个$M$行$N$列的矩阵中的每一个元素$X_iY_j$都代表一次AND操作）：

$$\text{位积矩阵}=\begin{bmatrix} X_{M-1}Y_{N-1}&X_{M-1}Y_{N-2}&\cdots &X_{M-1}Y_{0}\\ X_{M-2}Y_{N-1}&X_{M-2}Y_{N-2}&\cdots &X_{M-2}Y_{0}\\ \vdots&\vdots&\ddots&\vdots\\ X_{0}Y_{N-1}&X_{0}Y_{N-2}&\cdots &X_{0}Y_{0} \end{bmatrix}$$

最终乘积$Z$是这个矩阵中所有元素乘以其对应的二进制权重后的总和。矩阵中位于第$i$行、第$j$列的元素$X_{i}Y_{j}$的权重是$2^{i+j}$。

有符号数乘法

由于符号位有负的权重，所以 X 和Y 可以解构为：

X=-x_{m-1}2^{m-1}+\sum_{i=0}^{m-2} x_{i}2^{i} $$ $$ Y=-y_{n-1}2^{n-1}+\sum_{i=0}^{n-2} y_{i}2^{i}

由此，乘积结果可表示为：

$$XY = x_{m-1}y_{n-1}2^{m+n-2} + \sum_{i=0}^{i=n-2}\sum_{j=0}^{j=m-2} x_jy_i 2^{m+n-4} - \left(x_{m-1}\sum_{i=0}^{n-2}y_i 2^{m+i-1} + y_{n-1}\sum_{i=0}^{m-2}x_i 2^{n+i-1}\right)$$

难点在于出现了减法。在数字集成电路设计中，我们希望只使用加法器阵列。因此，必须利用补码的性质将“减法”转换为“加法”。

$$\begin{array}{ccccccccc} & & & & x_3 & x_2 & x_1 & x_0 & & \\ & & & & y_3 & y_2 & y_1 & y_0 & \\ \hline & & & & & x_2y_0 & x_1y_0 & x_0y_0 & & \\ & & & & x_2y_1 & x_1y_1 & x_0y_1 & & & \\ & & & x_2y_2 & x_1y_2 & x_0y_2 & & & & \\ & x_3y_3 & & & & & & 1 \\ & 1 & \overline{x_2y_3} & \overline{x_1y_3} & \overline{x_0y_3} & 1 & 1 & 1& \\ & 1 & \overline{x_3y_2} & \overline{x_3y_1} & \overline{x_3y_0} & 1 & 1 & 1& \\ + & & & & & & & 1 \\ \hline & S_6 & S_5 & S_4 & S_3 & S_2 & S_1 & S_0 \\ \end{array}$$

部分积的产生

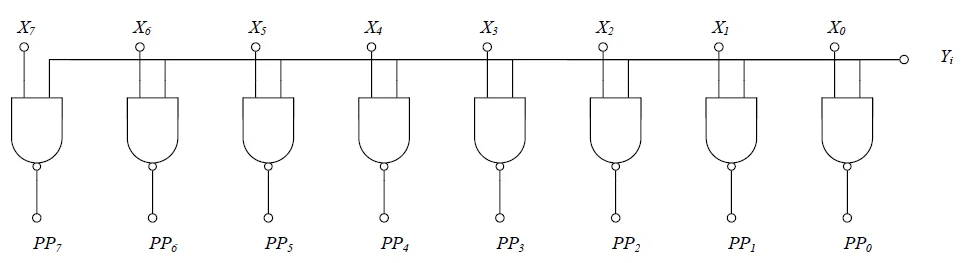
部分积产生电路

这里的与门使用的是 NAND ，由于加法器的反相特性，虽然NAND门的输出是AND门输出的反码，但后续的电路（如加法器）通常可以设计为接受反相输入，或者利用加法器本身的逻辑特性来抵消这个反相。

部分积压缩 — Booth 编码

如果乘数中某一位是0，该行部分积全为0，对结果无贡献。但我们无法控制输入数据中0的数量。

编码目标：通过对乘数进行编码，将连续的“1”序列转换为更稀疏的形式，从而减少实际需要运算的非零项数目。

每次乘数中取 $k$ 位（例如2位），即取： 00 、 01 、 10 、 11

改进的 Booth 编码

如果经典 Booth 编码每次取2位（基4 Booth），根据原本的二进制权重是 $1$ 和 $2$，组合起来可能出现 $1+2=3$ 的情况。

在硬件中，计算 $3 \times X$ 需要将 $X$ 左移一位（得到 $2X$）再通过加法器加上 $X$（得到 $3X$）。但是这个加法操作会带来延时。

在常规二进制中，权重只能是正的（$2^0, 2^1$）。但是改进的 Booth 编码将其扩展为带符号的数字集 如 $\{-2, -1, 0, 1, 2\}$。通过引入负系数，将 $3$ 重新编码。在更高基数下，可以将 $3$ 表示为 $4 - 1$。

其中：

• $4X$ 是左移两位（无延时）。

• $-1X$ 是取反加一（简单逻辑）。

$$2^{i+k-1} + 2^{i+k-2} + \dots + 2^i = 2^i(2^k - 1) = 2^{i+k} - 2^i$$

正常的逻辑是凑低位的相加得到任意数字（但是可能要加很多次，延时变长），但是现在思路换成：==无论连续的“1”有多长，我们都可以用一次高位加法和一次低位减法来替代中间所有的加法运算==。

部分积的累加

逐位进位阵列乘法器

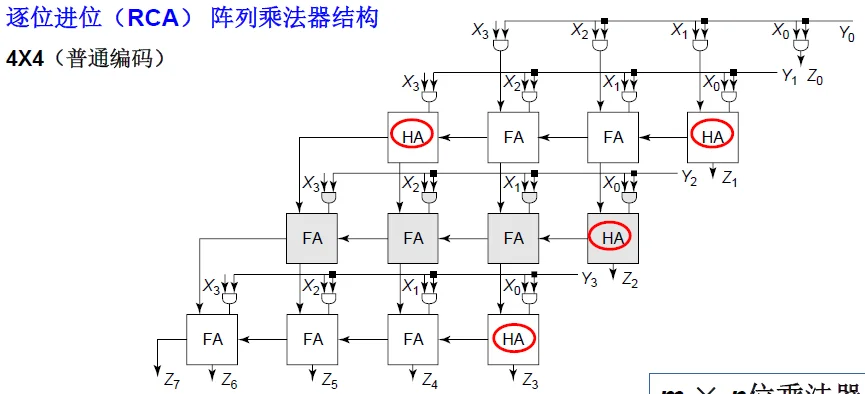
逐位进位阵列乘法器结构

• HA：半加器
• FA：全加器

第一行：

• $x_1y_0 + x_0y_1$：由于没有来自后面的进位，所以半加器就足够了

• $x_3y_1$：

最终相加

高性能乘法器架构

其他数据通路设计

移位器设计

移位操作

移位操作分类

• 逻辑移位：

  • 最基础的移位。无论左移还是右移，空出的位统一补0。主要用于无符号数的处理或单纯的位操作。

• 算术移位：

  • 主要用于有符号数（补码）的处理。

  • 算术右移是关键：为了保持负数的符号不变，右移时，高位（MSB）必须填充符号位。例如，负数 1100 右移一位应变为 1110，而不是 0110。

• 循环移位：

  • 数据像在圆环中移动，移出的位会被填补到另一端空出的位置，不会丢失数据。

ALU 设计

简单 TPU 设计

什么是TPU